- 土地の面積の求め方を知りたい。
- 手元の図面から三斜求積法で地積を計算したい。
こういった悩みに答えます。
結論は、三斜求積法を使えば専門知識不要で土地の面積を求めることができます。
本記事では、宅建士資格を有した行政書士が土地の面積が記載されていない図面から、おおよその面積を求める方法を解説します。
できるだけ簡単な方法ですので、小学生程度の算数知識でOKです。
鉛筆と定規(三角定規推奨)をご用意の上、記事を読み進めてみてください。
地積とは?
土地の面積のことを「地積」といいます。
面積を求めることを求積といい、求積表が載っている地積測量図等があれば、すぐに地積がわかります。
ですが、手元の図面に求積表がない場合は、ある方法を使うことで簡単におおよそのの面積を計算することができます。
なお、地積測量図について知りたい方はこちらの記事をご覧ください。
土地の面積の求め方は2通り
土地の面積の求め方は以下2通りあります。
- 「座標求積法」を使って地積を求める
- 「三斜求積法」を使って地積を求める
座標求積法を使って地積を求める
1つ目は「座標求積法」を使って土地の面積を求める方法。
現在の測量現場では、これが最もスタンダードで正確な求積法です。
測量では境界点(金属プレートやコンクリート杭がある点)の位置を座標値という数値を使って管理しており、それを使い求積します。
簡単に言うと、各座標値の位置関係から面積を計算する方法です。
計算方法は少々複雑なため、専用のソフトで計算するのが一般的です。
なお、単位は一般的には「メートル」ですが、小数点第3位まで表記するため、ミリ単位で管理されています。
そのため、求積もかなり正確に出ます。
また、現在法務局に提出する地積測量図はすべて座標値による座標求積表の記載が義務付けられています。
座標値がどういうものかのイメージはこちらの記事を参考にしてください。
三斜求積法を使って地積を求める
土地の面積の求め方2つ目は、「三斜求積法」という求積法。
測量現場ではこちらは少し古い方法のため、一般的ではありません。
とはいえ、建築図面などは未だに三斜求積法だったりするので、ある程度正確な面積を出すことは可能です。
今回のテーマである、手元の図面を使った、土地の面積の求め方は「三斜求積法」を使います。
簡単にいうと、土地の形状を複数の三角形に分割して面積を求める方法です。
ちょっと意味不明ですね。
以下でやり方の手順を詳しく解説します。
また、もし図面のPDFデータがあるなら、「Foxit PDF Reader」というフリーソフトを使うことでも、簡単に面積を計算することが可能です。
図面より土地の面積の求め方:手順
用意する必要があるのは、以下3つです。
- 図面(実際のサイズ)
- 鉛筆
- 定規(三角定規推奨)
図面は実際のサイズのものが必要です。縮小コピーや拡大コピーされた図面では面積を計算することはできません。
あとは線や数値を書き込む鉛筆と定規が必要です。
直角の線を書く必要があるため、三角定規が望ましいですが、カードや紙の角などで器用に直角線を引ければ、普通の定規でもなんとかなります。
また、電卓はあると便利ですが、筆算ができればなくても大丈夫です。
手順は次のように行います。
- 土地を三角形になるように分割
- 各三角形の底辺と高さを測る
- 実際の寸法に変換する
- 各三角形の面積を計算してすべて足す
以下で詳しく説明します。
1.土地を三角形になるように分割
今回は、こんな形をした土地の面積を図っていきます。
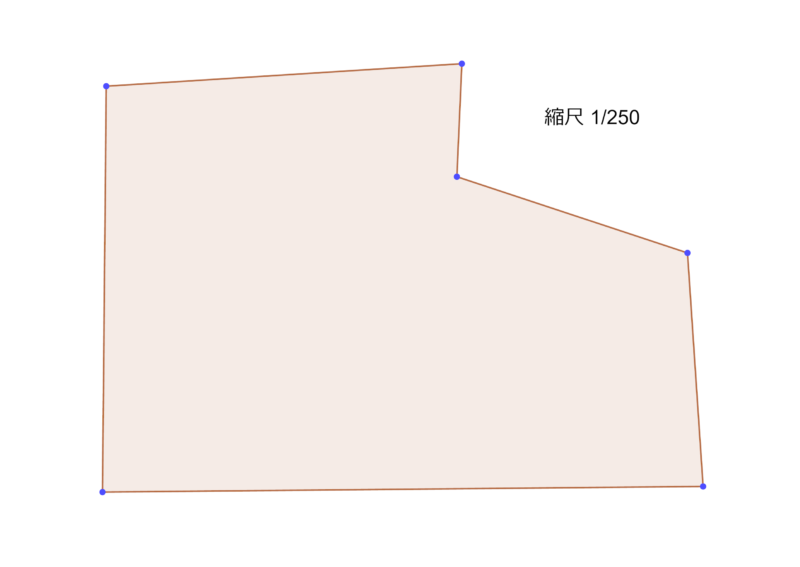
まず、土地を複数の三角形になるように分割します。
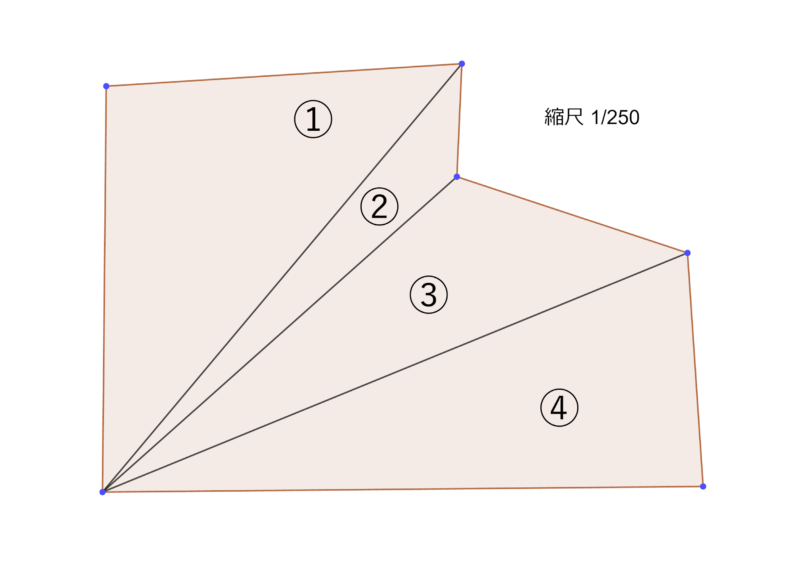
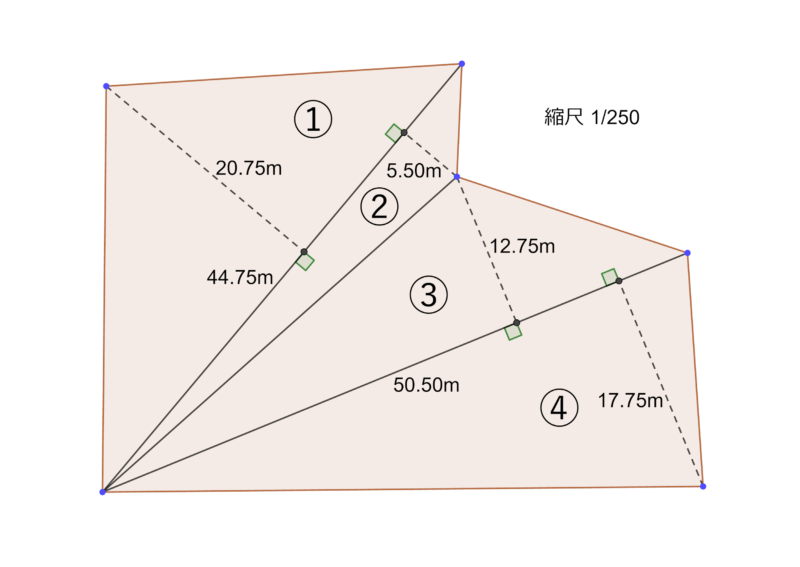
今回のケースだと次のように4つに分割できます。
2.各三角形の底辺と高さを測る
さらに、三角定規を使って、三角形の頂点から底辺に向けて直角に線を引いてください。
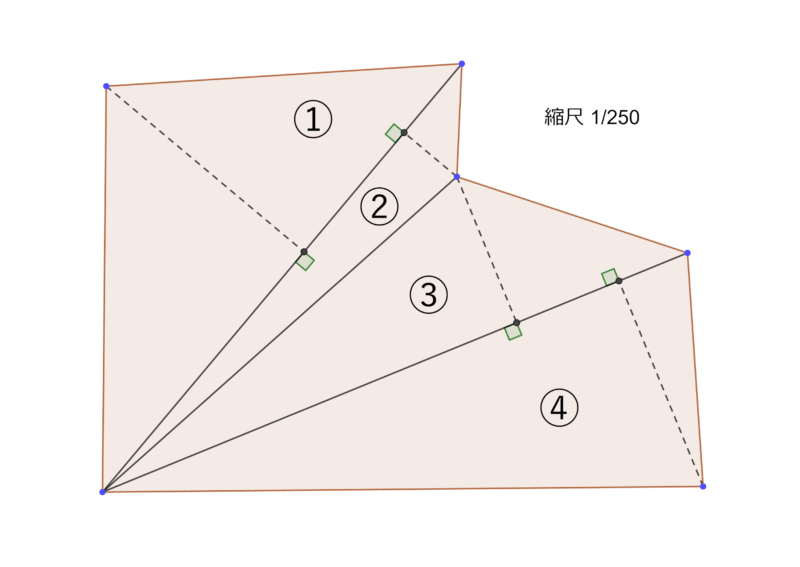
つまり、三角形の「底辺」と「高さ」の位置がわかるように線を引ければOKです。
線が引けたら、その線の長さを実際に図っていきます。
定規を使って、底辺と高さが何cmかわきに書き込んでください。
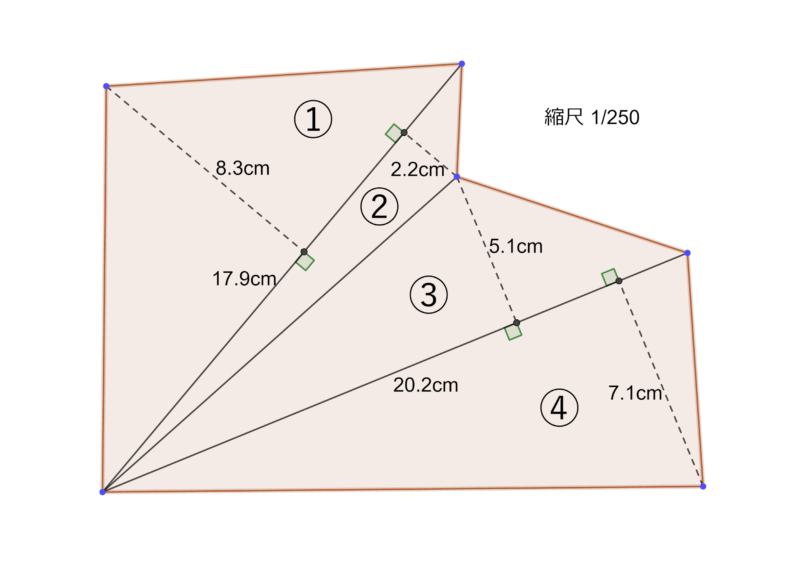
例えば、20cm2mmなら、20.2cmというふうに書き込めばOKです。
3.実際の寸法に変換する
次に図面上での長さ(cm)を実際の長さ(m)に変換していきます。
まず、図面に記載されている縮尺を確認してください。縮尺は「1/250」や「1:250」のような数値で、図面のどこかしらに書いてあるはずです。
なお、縮尺の分母が小さければ小さいほど、実寸に近くなるため正確に面積を求めることができます。
変換の公式は次のようになります。
「線の長さ(cm)×縮尺の分母÷100=実際の長さ(m)」
例の図面だと、縮尺は1/250ですので、図面上で長さが20.2cmだった場合、公式に当てはめると、実際の長さは「20.2cm×250÷100=50.50m」となります。
この計算が面倒くさい!という方は三角スケールという特殊な定規を買ってください。
三角スケールとは?
三角スケールとは、断面が三角形の定規です。
図面の縮尺に合わせて三角スケールをあてるだけで、実際の距離が測れる超便利な定規です。
不動産に携わる人なら絶対一本持っておくべきです。
土地家屋調査士用の三角スケールであれば、次の縮尺に対応しています。
- 1/100
- 1/200
- 1/250
- 1/300
- 1/500
- 1/600
4.各三角形の面積を計算してすべて足す
最後に各三角形の面積を求めて、全てを合計します。
三角形の面積は小学校の算数で習った公式「底辺×高さ÷2」を使います。
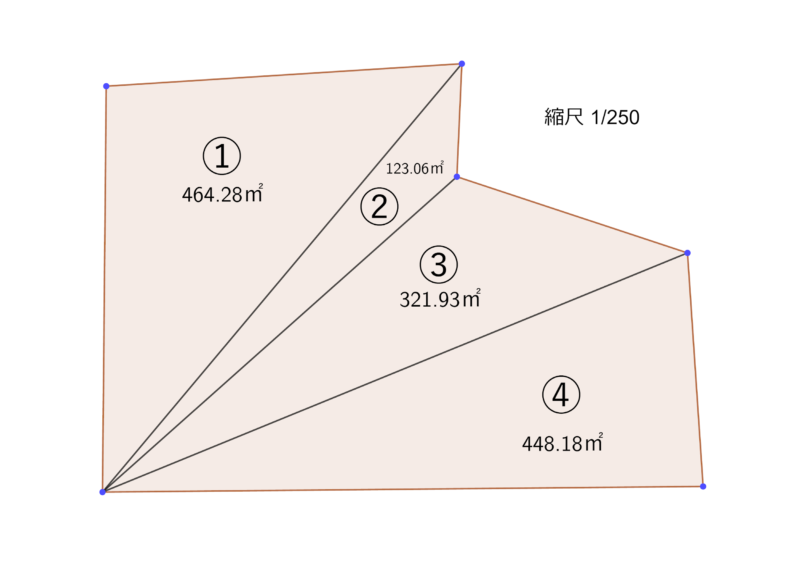
なお、単位は「㎡(平方メートル)」になります。
そして、これらすべてを足し合わせたものが、実際の土地の面積合計になります。
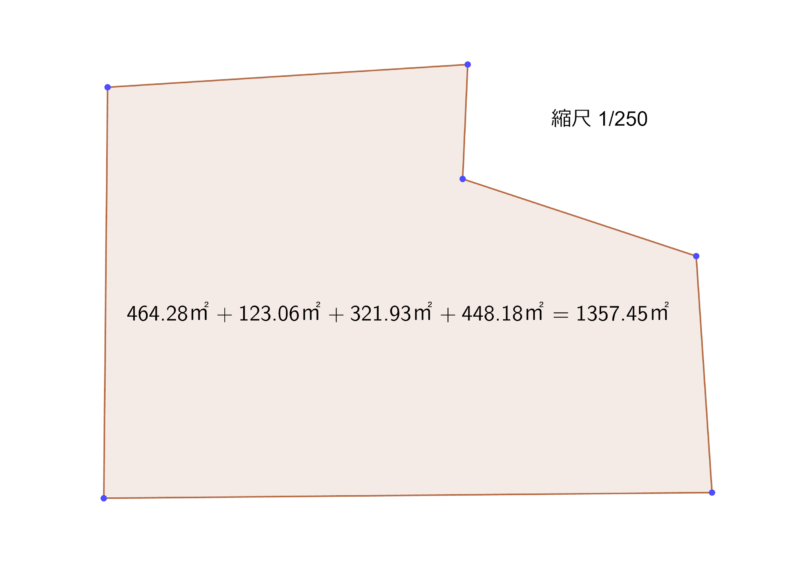
例だと、計算式はこんな感じ。
- ①の三角形:44.75m×20.75m÷2=464.28㎡
- ②の三角形:44.75m×5.50m÷2=123.06㎡
- ③の三角形:50.50m×12.75m÷2=321.93㎡
- ④の三角形:50.50m×17.75m÷2=448.18㎡
- ①+②+③+④の合計:464.28㎡+123.06㎡+321.93㎡+448.18㎡=1357.45㎡
㎡(平方メートル)から坪に変換する場合は?
1坪=約3.3㎡です。
もし、「㎡」から「坪」に変えたい場合は、先程の数値を「3.3」で割ればOKです。
1357.45㎡÷3.3=約411坪
土地の面積の求め方は三斜求積法が便利:まとめ
意外と簡単だったのではないでしょうか?
このようにすれば、例え面積のわからない土地でも、図面さえあれば求積することが可能です。
今回のポイントは以下の通りです。
- 土地を三角形に分割
- 三角形の面積を求める
- すべて合計する
もし、お手元に座標求積表が記載されている地積測量図をお持ちの方は、試しに今回の方法で求積して、面積が一致するか試してみてください。
思ったより正確なので驚くと思います。




※コメントは最大500文字、5回まで送信できます