- 測量とは何か?
- 測量のやり方を簡単に教えてほしい。
こういった疑問に答えます。
結論から言うと、測量現場では「角度と距離」を観測し、図面に「座標値」として表記します。
本記事では、宅建士資格を有した神奈川県の行政書士が一般的な測量である多角測量がどのような仕組み、手順で行われているのかを解説します。
簡単な図を使いながら、初心者でもできるだけわかりやすく説明しました。
本記事を参考にすれば、街でやっている測量がどういうものなのか分かるようになります。
どうぞご覧ください。
測量は道案内と同じ手順で位置関係を観測する
測量は道案内と似た手順でモノとモノの位置関係を測っていきます。
いきなり何を言ってるんだとお思いかもしれませんが、例えばあなたが町で道案内をすることを思い浮かべてください。
このような道があるとして、現在地からポストまでの道のりを案内します。
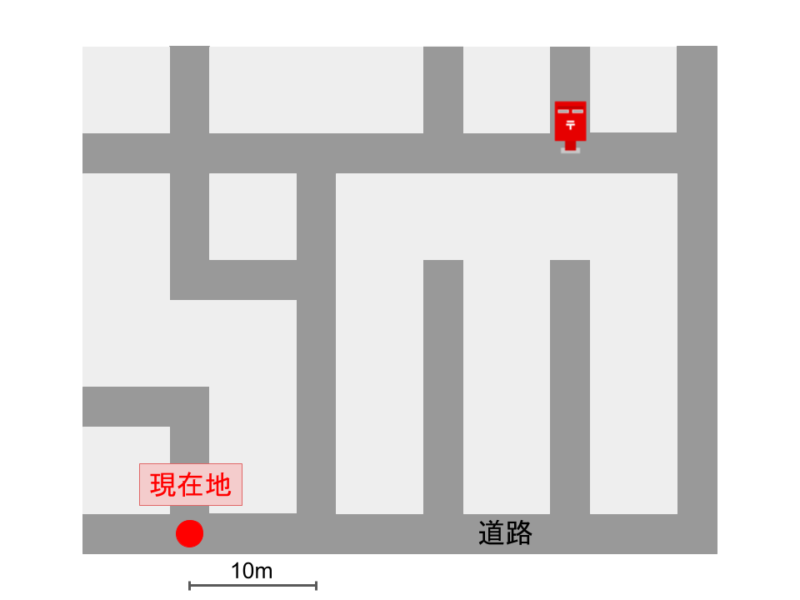
まず、地図の上側(北)を向いてるとします。
道順はおよそこんな感じになるかと思います。
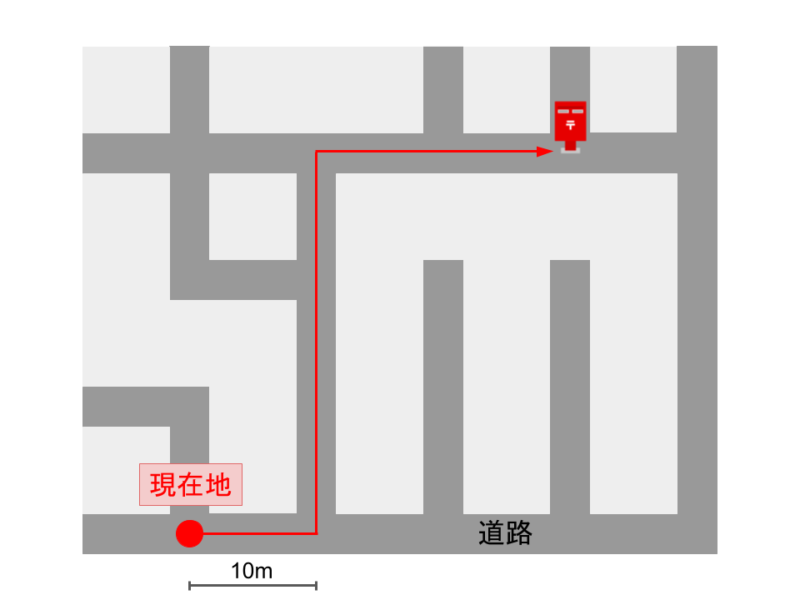
- 右向きに進み10m先の一つ目交差点を目指す
- 左折して突き当たりまでまっすぐ30mほど進む
- 右折して2ブロック行ったところにポストがある
測量でもこれと似た手順で「現在地からポストまでの位置関係」を測り、数値化していきます。
測量の一番の目的は位置関係を数値化すること
モノの位置関係を数値として表す方法としては以下2つがあります。
- 角度と距離
- 座標
順番に説明します。
角度と距離を測るのに必要な道具
一般的な測量は、「角度と距離」を計測していきます。
このような測量方法を多角測量(トラバース測量)と言い、最低限以下2つの道具を使います。
- 測量器械(トータルステーション)
- ミラー(プリズム)
順に解説します。
測量器械(トータルステーション)
測量器械(トータルステーション)は角度と距離同時に計測できる器械のことです。
以前は角度と距離を計測するには、別々の器械を使っていました。
- 角度を計測する器械:トランシット、セオドライト
- 距離を計測する器械:光波測距儀
しかし、現在はこの2つを同時に計測できるトータルステーションという測量器械を使うことがほとんどです。
トータルステーションは器械が向いている角度を表示させたり、レンズから光波(レーザー)を発射させることができます。
ミラー(プリズム)
ミラー(プリズム)とは、測量器械に向けて目標上に立てる道具です。
測量器械から発射された光波がミラーに反射し、器械に戻ってきます。
そのときの「光波のズレの量」を計測することで距離を求めます。
これらを組み合わせることで、基準となる角度0°から時計回りに角度◯◯°、距離◯◯mと位置を求めることが可能になります。
この時、器械を立てる点をトラバース点や器械点と言います。
図面上では「T1」や「T2」と表記し、三角「△」のマークで表します。
トラバース点についてはこちらの記事をご覧ください。
このトラバース点を数珠つなぎに測っていくことで位置関係を数値化していくのが測量です。
先程の道案内の例に当てはめてみます。
測量の角度と距離から位置関係を示す:具体例
流れとしてはこう。
- トラバース点に測量器械を立てる
- 角度0°を基準にして新たなトラバース点を観測
- 新たなトラバース点に器械を立てる
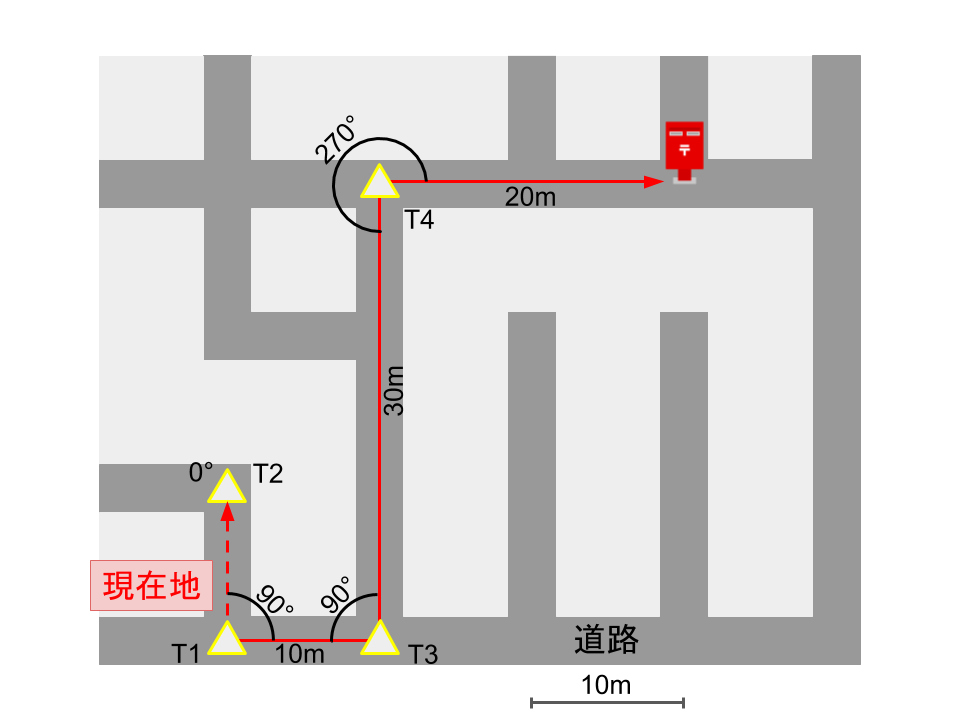
順番に説明します。
トラバース点に測量器械を立てる
まず「現在地」に鋲を打ち込みます。
打ち込んだ鋲をトラバース点「T1」とし、測量器械を立てます。
現場では目印にトラバース点を黄色く塗ります。
そして、もう一点鋲を打ち込み、これを「T2」とします。
そして「T2」にミラー(プリズム)を垂直に立てます。
「T1」に立てた測量器械を覗きながら、「T2」方向に測量器械を向けます。
覗くとこんな感じ。

この角度0°を基準(図の点線の矢印)とします。
これを「ゼロセット」や「バック」などと言います。
角度0°を基準にして新たなトラバース点を観測
次に測量器械を立てる場所「T3」に鋲を打ち込み、ミラー(プリズム)を立てます。
そして、測量器械を向けます。
「T1」から「T2」の角度0°の基準(点線の矢印)から時計回りに角度が何°かが表示されます。
そして、測量器械の「測距」ボタンを押すと光波が出て、表示されている角度と距離が記録されます。
例だと「器械T1立てのT2バックでT3は角度90°、距離10m」となります。
なお、実際の測量器械は角度は「秒(″)」、距離は「mm」まで計測されます。
- 角度:90°00′00″
- 距離:10.000m
新たなトラバース点に器械を立てる
先程の手順で「T3」の位置関係を観測することができました。
今度は、「T1」の位置から見えないポイントを観測するため、「T3」に新たに測量器械を立てます。
あとは同じ手順です。
- T3(器械点)→T1(バック)を角度0°としT4を観測すると角度90°、距離30m
- T4(器械点)→T3(バック)を角度0°とし目標(ポスト)を観測すると角度270°、距離20m
図面上では座標値を使用する
ここまでで、「角度と距離」を使って位置関係を表すことができました。
しかし、「角度と距離」は基準となる0°をいちいち示さないといけないため、これだと不便です。
そのため、現在は「角度と距離」の観測データを「座標値」に変換し図面に記載します。
- 角度と距離:相対的
- 座標値:絶対的
法務局保管の図面である地積測量図は昔は「角度と距離」のみの表記でしたが、現在は座標値が載っています。
地積測量図の歴史についてはこちらの記事をご覧ください。
座標とは
座標とはX軸とY軸がある二次元座標のことです。
数学でも勉強したと思いますが左下が(X=0,Y=0)の原点になります。
ただ、測量系の座標は数学系とは違い、縦がX軸、横がY軸となることに注意してください。
- 数学系の座標:縦がY軸、横がX軸
- 測量系の座標:縦がX軸、横がY軸
角度と距離を座標値に変換する:具体例
「角度と距離」の観測データをパソコンで計算することで座標値を求めます。
今回の例を実際に当てはめてみてみましょう。
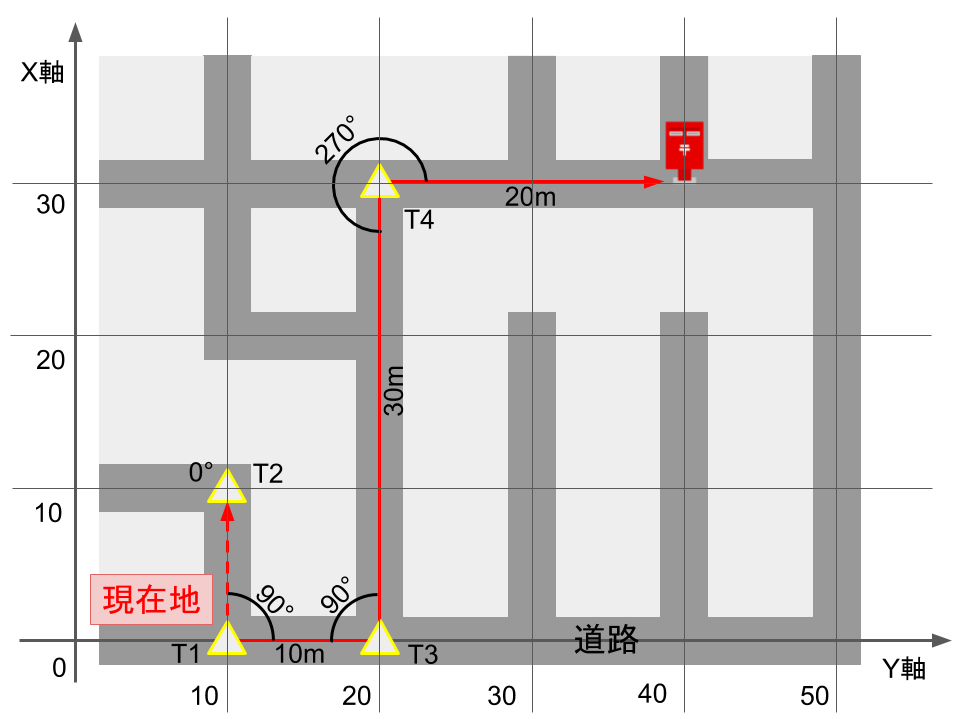
左下が原点(X=0,Y=0)となります。
順に以下のようになります。
- T1(現在地):(X=0,Y=10)
- T2:(X=10,Y=10)
- T3:(X=0,Y=20)
- T4:(X=30,Y=20)
- ポスト:(X=30,Y=40)
任意座標系と世界測地系
また、細かく分けると測量の座標系は2種類あります。
- 任意座標系
- 世界測地系
任意座標系
原点(X=0,Y=0)の位置を任意で設定した座標系です。
先程の道案内の例は任意座標系です。
例だと、T1より10m西側のポイントを原点(X=0,Y=0)としました。
ところが、T1を原点(X=0,Y=0)と設定した場合、座標値はこのようにY軸で10mずつ数値が小さくなります。
- T1(現在地):(X=0,Y=0)
- T2:(X=10,Y=0)
- T3:(X=0,Y=10)
- T4:(X=30,Y=10)
- ポスト:(X=30,Y=30)
例え、どこに原点を設定したとしても位置関係は変わることがないため、上記2つの座標値は同じだと言えます。
なお、メリットとしては座標値の桁数を少なくすることができるため見やすいです。
一方、デメリットとしては完全に絶対的なものではないということがあげられます。
また、こちらは任意座標系の地積測量図です。
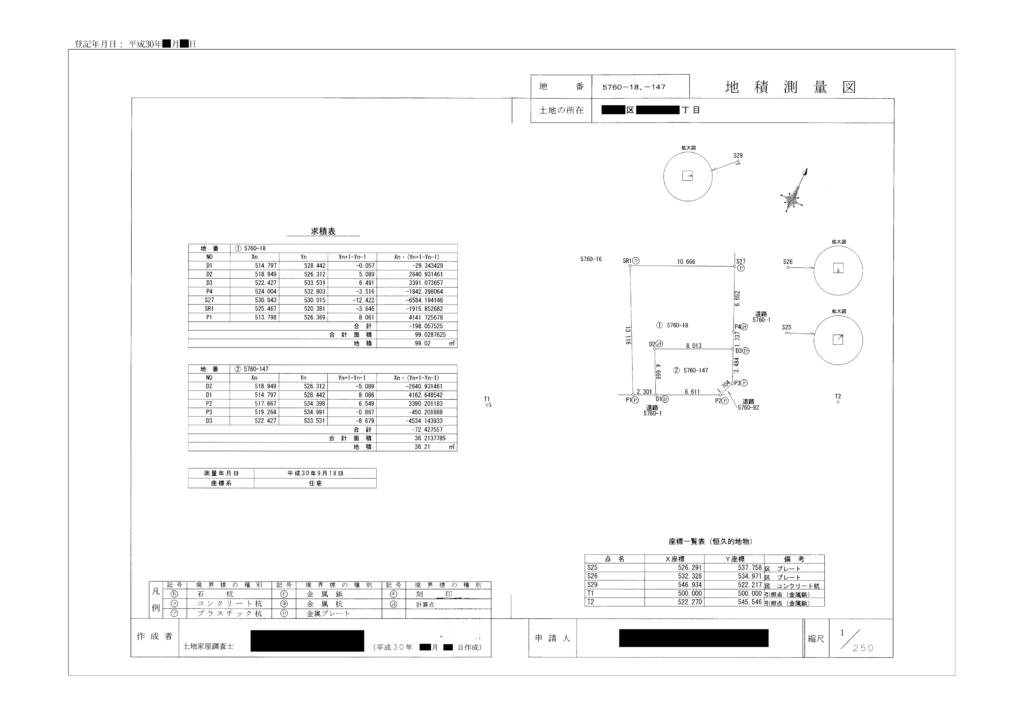
世界測地系
世界測地系とは、全世界共通で位置を特定することが可能な座標系のことです。
世界測地系の座標値で表した「点」は世界中ただ一つとなるため、絶対的なものと言えます。
以下が世界測地系の地積測量図
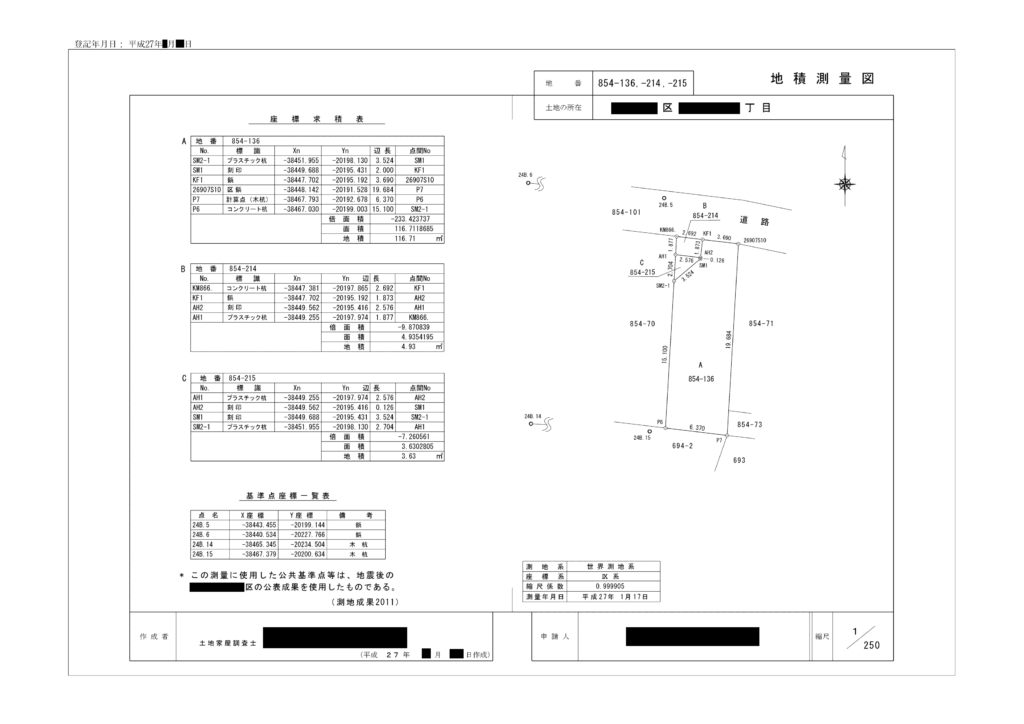
メリットは、震災などで境界標が動いてしまったり、そもそも無くなってしまった場合も、正確な位置に復元することが可能なことです。
一方、デメリットは世界測地系の公共基準点(器械点)が近くにない場合などは遠くから繋げる必要があり、測量費用が高くなることと、世界測地系の座標値は桁数が多いため、管理が面倒になることです。
測量とは何か?:まとめ
今回は測量とは何か?を具体例を出してできるだけ簡単に説明しました。
以下にポイントをまとめると次のようになります。
- 必要な道具
- 測量器械(トータルステーション)
- ミラー(プリズム)
- 測量の手順
- 現地にて「角度と距離」を使い位置関係を観測
- 観測データを座標値に変換
測量はこの手順の繰り返しでモノとモノの位置関係を数値化していくのです。
境界標について詳しく知りたい方はこちらの記事をご覧ください。




※コメントは最大500文字、5回まで送信できます